Answer: 0.65 represents the initial number of people in hundreds of thousands .
Also ,
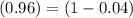
It means the rate of decay = 0.04=4%
Explanation:
Given: The function
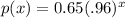 models the number of people in hundreds of thousands where x represents the number of 10-minute periods since the trend has been observed.
models the number of people in hundreds of thousands where x represents the number of 10-minute periods since the trend has been observed.
We know that the exponential decay function is given by :-
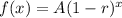 , where A is the initial amount and r is the rate of decay in time x.
, where A is the initial amount and r is the rate of decay in time x.
As compared to the given function we get
A = 0.65
It means the initial number of people = 0.65 hundreds of thousands =
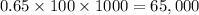
Also ,
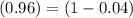
Hence, the rate of decay = 0.04=4%