Question

Please help! I’ve see a couple a different answers and I’m getting even more confused.>>Consider the equation log(3x-1)=log28. Explain why 3x-1 is not equal to 8. Describe the steps you would take to solve the equation, and state what 3x-1 is equal to.

Answer 1

Consider the equation:
`\log (3x-1) = \log_2 8`

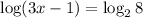
Since, the functions:
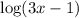`\log (3x-1)` has a base of 10 and
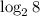`\log_2 8` has a base of 2.

By logarithmic properties:

`\log_a x = \log_a y`

⇒
`x = y`

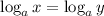
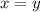
Since, these logarithmic functions have different bases they does not satisfy the logarithmic properties

⇒
`(3x-1) \\eq 8`

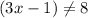
Solve the equation:
`\log (3x-1) = \log_2 8`

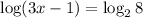
By Properties of logarithmic:

`\log_a x^n = n \log _a x`

`\log_b b = 1`

`\log_b x = a` ⇒
`x = b^a`

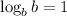
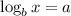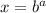
Using these properties to solve the given equation as shown below:

`\log (3x-1) = \log_2 2^3`

`\log (3x-1) =3 \log_2 2`

`\log (3x-1) = 3`

`(3x-1) = 10^3`

`(3x-1) = 1000`

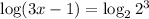
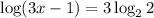
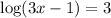
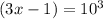
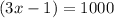
Therefore, (3x -1) is equal to 1000