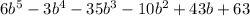Question

(3b^3-4b^1-7)(2b^2-b^1-9)

*Multiplying Polynomials *

Answer 1

`6b^(5)-3b^(4)-35b^(3)-10b^(2)+43b+63`

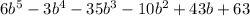
Explanation:

we have to find the multiplication of following polynomials

As we know that the multiplication of two polynomials are done in following way

let we have two polynomial (ax+b) and (cx+d) their product would be

(ax+b)(cx+d)

=ax(cx+d)+b(cx+d)

=acx² + axd + bcx + bd

Now similarly for the given polynomial we have

`(3b^(3)-4b-7)*(2b^(2)-b-9)`

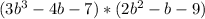
it could be written as

=3b³(2b²-b-9) -4b(2b²-b-9) -7(2b²-b-9)

Multiplying inside with values

=
`6b^(5)-3b^(4)-27b^(3)-8b^(3)+4b^(2)+36b-14b^(2)+7b+63`

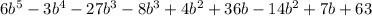
Combining same values

=
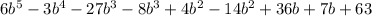
`6b^(5)-3b^(4)-27b^(3)-8b^(3)+4b^(2)-14b^(2)+36b+7b+63`

=
`6b^(5)-3b^(4)-35b^(3)-10b^(2)+43b+63`