Question

How to solve part ii and iii

Answer 1

(i) Given that

`\tan^(-1)(x) + \tan^(-1)(y) + \tan^(-1)(xy) = (7\pi)/(12)`

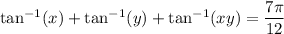
when
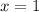`x=1` this reduces to

`\tan^(-1)(1) + 2 \tan^(-1)(y) = (7\pi)/(12)`

`\frac\pi4 + 2 \tan^(-1)(y) = (7\pi)/(12)`

`2 \tan^(-1)(y) = \frac\pi3`

`\tan^(-1)(y) = \frac\pi6`

`\tan\left(\tan^(-1)(y)\right) = \tan\left(\frac\pi6\right)`

`\implies \boxed{y = \frac1{\sqrt3}}`

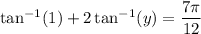
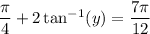
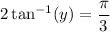
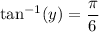
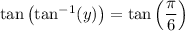
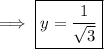
(ii) Differentiate
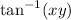`\tan^(-1)(xy)` implicitly with respect to
`x`. By the chain and product rules,

`\frac d{dx} \tan^(-1)(xy) = \frac1{1+(xy)^2} * \frac d{dx}xy = \boxed{(y + x(dy)/(dx))/(1 + x^2y^2)}`

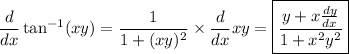
(iii) Differentiating both sides of the given equation leads to

`\frac1{1+x^2} + \frac1{1+y^2} (dy)/(dx) + (y + x(dy)/(dx))/(1+x^2y^2) = 0`

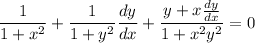
where we use the result from (ii) for the derivative of
`\tan^(-1)(xy)`.

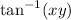Solve for
`(dy)/(dx)` :

`\frac1{1+x^2} + \left(\frac1{1+y^2} + \frac x{1+x^2y^2}\right) (dy)/(dx) + \frac y{1+x^2y^2} = 0`

`\left(\frac1{1+y^2} + \frac x{1+x^2y^2}\right) (dy)/(dx) = -\left(\frac1{1+x^2} + \frac y{1+x^2y^2}\right)`

`(1+x^2y^2 + x(1+y^2))/((1+y^2)(1+x^2y^2)) (dy)/(dx) = - (1+x^2y^2 + y(1+x^2))/((1+x^2)(1+x^2y^2))`

`\implies (dy)/(dx) = - ((1 + x^2y^2 + y + x^2y) (1 + y^2) (1 + x^2y^2))/((1 + x^2y^2 + x + xy^2) (1+x^2) (1+x^2y^2))`

`\implies (dy)/(dx) = -((1 + x^2y^2 + y + x^2y) (1 + y^2))/((1 + x^2y^2 + x + xy^2) (1+x^2))`

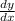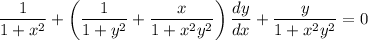
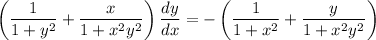
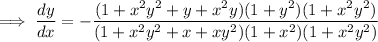
From part (i), we have
`x=1` and
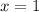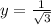`y=\frac1{\sqrt3}`, and substituting these leads to

`(dy)/(dx) = -\frac{\left(1 + \frac13 + \frac1{\sqrt3} + \frac1{\sqrt3}\right) \left(1 + \frac13\right)}{\left(1 + \frac13 + 1 + \frac13\right) \left(1 + 1\right)}`

`(dy)/(dx) = -\frac{\left(\frac43 + \frac2{\sqrt3}\right) * \frac43}{\frac83 * 2}`

`(dy)/(dx) = -\frac13 - \frac1{2\sqrt3}`

as required.