Answer:
option D is correct
time will the ride take = 150 minutes
Explanation:
Using formula:
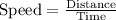 .....[1]
.....[1]
As per the given condition:
Zachary's mother take time to rider her bike to the market = 25 minutes.
and the distance of the market away =
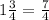 miles.
miles.
Then, substitute these value in [1] , we have;
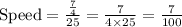 miles per minutes.
miles per minutes.
It is also given that , if she rides with the same speed to the park that is
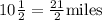 away.
away.
To find how long will the ride take.
Using the same formula to find the time;
Let the time be t.
we have;
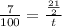
By cross multiply, we have;
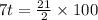
Simplify:
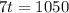
Divide by 7 both sides we get;
t = 150 minutes.
Therefore, 150 minutes will the ride take.