Answer:
Length of segment BC = 24 cm
Explanation:
It is given that AC is a diameter and B is a point on the circle P.
So, Δ ABC is a triangle in a semicircle and hence ∠ B = 90° as angle in a semicircle is a right angle.
It is also given that the length of the radius is 13 cm.
Therefore, diameter AC = 2 × radius = 2(13) = 26 cm.
It is given that AB = 10 cm.
From the right triangle Δ ABC,
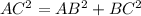
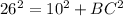

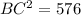
BC = 24 cm