Answer:
Option D is correct.
Side EG = 24 units.
Explanation:
As per the given statement:
In a parallelogram EFGH
 and
and
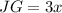
By Properties of parallelogram:
- Two diagonals bisects each other and
- Each diagonal of a parallelogram separates it into two congruent.
Here, EG and FH are diagonals;
EG = EJ + JG
by properties of parallelogram:
EJ =JG
Substitute the given values we have;
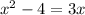
⇒

⇒
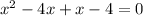
⇒
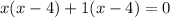
⇒
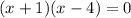
By zero product property;
x = -1 and x = 4
⇒
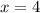 (always used positive number for sides)
(always used positive number for sides)
Then;
EG = JG+JG = 2JG
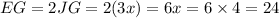 units
units
Therefore, the diagonal EG = 24 units.