Answer:
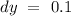
Explanation:
Considering the Leibniz notation to represent the derivative of
 with respect to
with respect to
 , suppose
, suppose
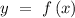 is a differentiable function, let
is a differentiable function, let
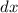 be the independent variable such that it can be designated with any nonzero real number, and define the dependent variable
be the independent variable such that it can be designated with any nonzero real number, and define the dependent variable
 as
as
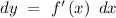 ,
,
where
 is the function of both
is the function of both
 and
and
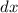 . Hence, the terms
. Hence, the terms
 and
and
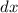 are known as differentials
are known as differentials
Dividing both sides of the equation by
 , yield the familiar expression
, yield the familiar expression
 .
.
Given that
 and
and
 , hence
, hence
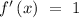 .
.
Subsequently,
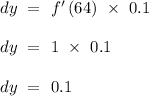 .
.