Question

The object of the game is to toss a beanbag in the circular hole of a 48-by-24-inch board. If the diameter of the circle is 6 inches, what is the geometric probability an object will hit the circle on the board? Assume that the object will hit the board.

Answer 1

Geometric probability of an object hitting a circular hole is 0.0245.

Explanation:

We have given,

A board of size 48 by 24 inch. There is a circular hole in the board having diameter 6 inches.

So,

Area of a board = 48 × 24 = 1152 square inches

And area of circular hole = π×r² {where r = diameter/2 = 6 / 2 = 3 inches}

Area of circular hole = π×3² = 9π = 28.27 square inches

Now, we need to find the geometric probability of an object will hit the circle.

Geometric probability = Area of circular hole / Area of board

Geometric probability =
`(28.27)/(1152)`

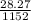
Geometric probability = 0.0245

hence geometric probability of an object hitting a circular hole is 0.0245.