Answer:
Triangles must be similar
Explanation:
We are given two triangles
First triangle:
sides are 6 , 9 , 12
Second triangle:
2.5, 3.75 , 5
We know that if two triangles are similar , then their ratio of sides must be equal
so, we will find ratio of side of each corresponding sides
and then we check whether they are equal
we get
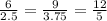
now, we can find each ratios and check whether they are equal
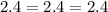
we can see that
all values are equal and same
so, the ratio of their sides are equal
Hence , triangles must be similar