Answer:
1. 30
2. 150
Explanation:

Lets assume tan(x) = u
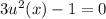
Now we solve for 'u'
add 1 on both sides
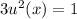 , divide both sides by 3
, divide both sides by 3
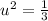
Take square root on both sides
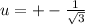
We replace tan(x) for 'u'
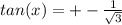
x = 30 because
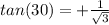 in first quadrant
in first quadrant
x = 30 (tan is positive in first quadrant)
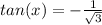
x = 150 because
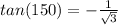 in second quadrant
in second quadrant
tan is negative in second quadrant