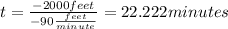Answer:
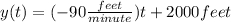
Explanation:
Given the linear function in the form

We are going to represent the situation using the linear function.
We are going to call the variable ''x'' time. We can write x = t ⇒
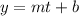
 will be the altitude function that depends on the variable ''t'' that is time in minutes.
will be the altitude function that depends on the variable ''t'' that is time in minutes.
In the instant
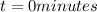 the hot air balloon has an altitude of 2000 feet ⇒
the hot air balloon has an altitude of 2000 feet ⇒
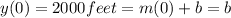 ⇒
⇒
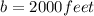
We can think that the slope ''m'' is the constant rate of the function.
Given that the hot air balloon descends,
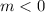 ⇒
⇒
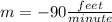
Now we write the function :
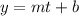
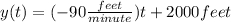
For example, when t = 0 ⇒

Or if we want to find the time when the hot air balloon finally descends :