Question

1. The edge lengths of a right rectangular prism are

1
2
meter,
1
2
meter, and
3
4
meter. How many unit cubes with edge lengths of
1
12
meter can fit inside?

2. The base of a rectangular prism has an area of
1
8
ft2, and the height of the prism is
2
3
ft. What is the volume of the prism?

3. The edge lengths of a right rectangular prism are
2
3
meter,
1
4
meter, and
3
4
meter. How many unit cubes with edge lengths of
1
10
meter can fit inside?

Answer 1

1) 324 cubes can be fitted into the rectangular prism.

2) 1/12 cubic ft.

3) 125 cubes can be fitted into the rectangular prism.

Explanation:

1)

The edge lengths of the prism are given as:

1/2 meter, 1/2 meter and 3/4 meter.

The formula for finding the volume of a rectangular prism is the following: Volume = Length×Height×Width, or V = L×H×W.

so here let L=1/2 meter, B=1/2 meter and H=3/4 meter

Hence, V=(1/2)×(1/2)×(3/4)=3/16 cubic meters.

Now let 'n' cubes can be fitted inside this rectangular prism.

Let 'v' denotes the volume of 1 cube.

Volume of a cube with side length 's' units is given by:

`v=s^3 cubic units.`

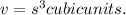
Here s=1/12 meter

Hence, volume of cube (v)=(1/12)×(1/12)×(1/12)=1/1728 cubic meter

Now V=n×v

`n=(V)/(v)\\\\n=((3)/(16))/((1)/(1728))\\\\\\n=(3* 1728)/(16)\\\\n=324`

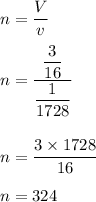
Hence, 324 cubes can be fitted into the given rectangular pyramid.

2)

The base of a rectangular prism has an area of 1/8 square feet.

This means let the rectangular base has length L and base B such that L×B=1/8 square feets.

also height (H) of the rectangular prism=2/3 ft.

Hence volume of rectangular prism= L×B×H=(1/8)×(2/3)=1/12 cubic ft.

3)

The edge lengths of the prism are given as:

2/3 meter, 1/4 meter and 3/4 meter.

The formula for finding the volume of a rectangular prism is the following: Volume = Length×Height×Width, or V = L×H×W.

so here let L=2/3 meter, B=1/4 meter and H=3/4 meter

Hence, V=(2/3)×(1/4)×(3/4)=1/8 cubic meters.

Now let 'n' cubes can be fitted inside this rectangular prism.

Let 'v' denotes the volume of 1 cube.

Volume of a cube with side length 's' units is given by:

`v=s^3 cubic units.`

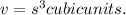
Here s=1/10 meter

Hence, volume of cube (v)=(1/10)×(1/10)×(1/10)=1/1000 cubic meter

Now V=n×v

`n=(V)/(v)\\\\n=((1)/(8))/((1)/(1000))\\\\\\n=(1000)/(8)\\\\n=125`

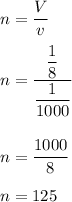
Hence, 125 cubes can be fitted into the given rectangular pyramid.