Question

Given: ∠1 , ∠2 , ∠3 , and ∠4 formed by two intersecting segments.

Prove: ∠2 and ∠4 are congruent.

(look at image down below)

Answer 1

1.
`\angle 2+\angle 3=180^(\circ)`

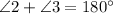
2.Linear postulate

3.
`\angle 2+\angle 3=\angle 3+\angle 4`

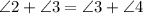
4.Subtraction property of equality

Step-by-step explanation:

We are given that angle 1. angle 2, angle 3 and angle 4 formed by two intersecting segment.

We have to prove that angle 2 and angle 4 are congruent.

Proof:

Statement 1:
`\angle 1,\angle 2,\angle 3` and
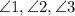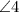`\angle 4` formed by two intersecting lines.

Reason: Given

Statement 2:
`\angle 3` and
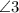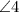`\angle 4` forms linear pair

Reason:By definition of linear pair

Statement 3:
`\angle 2` and
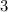`3` forms linear pair

Reason: By definition of linear pair

Statement 4:
`\angle 2+\angl 3=180^(\circ)`

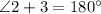
Reason: Linear pair postulate

Statement 5:
`\angel 3+\angle 4=180^(\circ)`

Reason: Linear pair postulate

Statement 6:
`\angle 2+\angle 3=\angle 3+\angle 4`

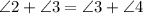
Reason: By substitution property of equlaity

Statement 7:
`\angle 2=\angle 4`

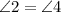
Reason: Subtraction property of equality