Answer:
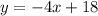
Explanation:
Let x be the number of hours.
We have been given that a vat contains 18 gallons of liquid when a drain pipe opens and the liquid begins to leave the vat at a rate of 4 gallons per hour.
To graph the amount of liquid first of all we will find the equation of line for our given situation.
Since we know that equation of a line in slope-intercept form is:
 , where, m = slope and b = y-intercept or initial value.
, where, m = slope and b = y-intercept or initial value.
As liquid is leaving the vat at a rate of 4 gallons per hour, this means that amount of liquid in vat in decreasing 4 gallons per hour. As slope is also known as rate of change, so slope of our given line will be -4. A negative slope means that with each increase in x our y will decrease by 4.
As initially there were 18 gallons of liquid in vat, so our y-intercept will be 18.
Upon substituting our given values in slope-intercept form of equation we will get,
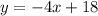
Let us find x-intercept by substituting y=0 in our equation.
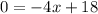

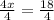
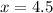
Now we will draw a line connecting our y-intercept and x-intercept from (0,18) to (4.5,0).
Please find the attachment for the graph of the given line.