Question

20 points

Graph.

y+4=2/5(x−3)

Use the Line Tool and select two points to graph the equation. Use the slope and the point provided in the equation.

Answer 1

`y+4=(2)/(5)(x-3)`

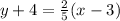
This is a point-slope interception, where we can deduct the slope and one point.

So, from the given expression, one points on the line is
`A(3,-4)`.

The slope is
`(2)/(5)`.

Also, we can find another point, where
`x=0`.

`y+4=(2)/(5)(0-3)\\y+4=(2)/(5)(-3)\\ y=-(6)/(5)-4\\ y=(-6-20)/(5) =-(26)/(5) \approx -5.2`

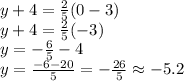
So, the other point is
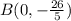`B(0,-(26)/(5))`. Now, we can graph.

In the image attached you can observe the y-intercept and the x-intercept. Those are the two common points we tend to use to graph linear functions like this one. Also, observe that the line is really inclined, this is because in the given slope, the numerator (y values) represents a lower variation.

Answer 2

slope is

`m=(2)/(5)`

First point is

x1=5 ,y1=-4

Second point is

x2=0 , y2=-6

Explanation:

We are given equation of line as

`y+4=(2)/(5)(x-5)`

Firstly, we can find slope and a point

we can compare it with point slope form of line

`y-y_1=m(x-x_1)`

we get

x1=5 ,y1=-4

so, one point is (5,-4)

slope is

`m=(2)/(5)`

we can find second point

We can plug x=0

and find y

`y+4=(2)/(5)(0-5)`

`y=-6`

so, we get

other point is (0,-6)

now, we can draw graph