Question

Which is equivalent to after it has been simplified completely? Assume n ≠ 0.
PICTURE BELOW

Answer 1

We have been given an expression
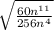`\sqrt{(60n^(11))/(256n^4)}`. We are asked to simplify our given expression.

First of all, we will simplify the expression inside radical as:

`\sqrt{(15n^(11))/(64n^4)}`

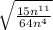
Using exponent property
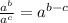`(a^b)/(a^c)=a^(b-c)`, we will get:

`\sqrt{(15n^((11-4)))/(64)`

`\sqrt{(15n^(7))/(64)`

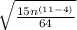
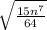
Now we will use exponent property
`\sqrt{(a^b)/(a^c)}=(√(a^b))/(√(a^c))`.

`(√(15n^7))/(√(64))`

`(√(15n\cdot n^6))/(√(8^2))`

`(√(15n\cdot (n^3)^2))/(√(8^2))`

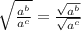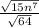
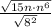
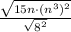
Now we will bring out perfect squares from radical as:

`(n^3√(15n))/(8)`

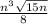
Therefore, simplified form of our given expression would be
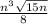`(n^3√(15n))/(8)` and option B is the correct choice.

Answer 2

Option B

Explanation:

Given is a term under square root sign.

Inside square root is given a rational function in n as

`(60n^(11) )/(256n^(4) )`

Simplify constant terms and n terms separately to get

=
`(15n^7)/(64) \\=(n^3)/(8) √(15n)`

Out of the four options option 2 matches with this.

Hence correct answer is option B.