Question

Select the graph for the solution of the open sentence. Click until the correct graph appears. 2|x| < 4

Answer 1

The correct graph would be the one with open circles on -2 and 2 and shaded between those two dots.

Explanation:

2|x| < 4

-divide both sides by 2

|x| < 2

x < 2 or x > -2

:)

Answer 2

We have to plot the graph of the inequality:

`2|x|<4`

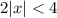
i.e.
`|x|<2`

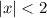
the graph is a number line representing the possible values of 'x' by solving the inequality.

the inequality is solved as:

-2<x<2

i.e. the region is: (-2,2); i.e. we have all the real values between -2 and 2 such that 2 and -2 is not included hence there is a open circle at 2 and -2.

the graph of the solution is attached to the answer.