Answer:
Given sides 12, 16 and 20 can be the sides of right triangle.
Explanation:
Sides of right triangle always follow the Pythagoras theorem.
i.e
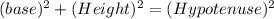
For the given Lengths 7, 40 and 41
We need to check if
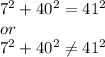
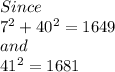
That means,

hence 7,40 and 41 can not be the sides of right triangle.
Next,
Given sides 12,16 and 20.
Again follow the similar process used in the above problem.
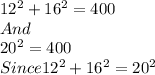
Therefore given sides 12,16 and 20 can be the sides of right triangle.