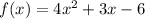Question

What is the equation in standard form of a parabola that models the values in the table x -2,0,4 f(x) 4,-6,70

3x^2+4x-6
4x^2+3x-6
4x^2-3x-6
4x^2-3x-6
-4x^2-3x-6

Answer 1

it is going to be 4x^2 + 3x -6

Answer 2

Equation of parabola is :
`f(x) = 4x^2 + 3x -6`

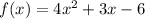
Explanation:

Given,

x = -2 0 4

f(x) = 4 -6 70

General equation of parabola is:
`y = ax^2 + bx + c`

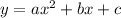
Now we plug corresponding x and y values to get coefficient a,b and c.

Fro x =-2 and y( =f(x) ) = 4

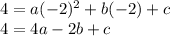`4 = a(-2)^2 + b(-2) + c\\4 = 4a -2b + c` ______(1)

For x = 0 , y = -6

`-6 = a(0)^2 + b(0) + c\\-6 = c` _____(2)

For x = 4 , y = 70

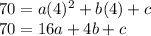`70 = a(4)^2 + b(4) + c\\70 = 16a + 4b + c` _____(3)

Plug c= - 6 in equation (1) and (3)

We get,
`4 = 4a - 2b - 6  \\And\\70 = 16a + 4b - 6`

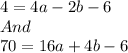
solving above two equations to find a and b.

Multiply equation (1) by 2 then add equation (1) and (3)

`8 + 70 = 8a + 16a -4b + 4b -12 -6\\78 = 24a - 18\\78 + 18 = 24a\\a = 96/24 = 4\\And b = 3`

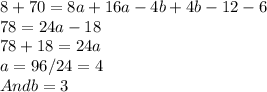
Hence equation of parabola is :
`f(x) = 4x^2 + 3x -6`