Question

How will adding the value of 75 affect the mean and median of data set 1,5,7,9,9,10

Answer 1

After adding 75 the mean and median has increased but mean increased more than median.

Explanation:

We have been given a data set: 1, 5, 7, 9, 9, 10. We are asked to find how adding a data point 75 will change the mean and median of our given data set.

Since we know that adding an extreme large data point to a data set increases the mean, while median is less affected by outliers.

Let us find the mean and median of given data set.

`\text{Mean}=\frac{\text{Total of the values of a data set}}{\text{Total number of data points}}`

`\text{Mean}=(1+5+7+9+9+10)/(6)`

`\text{Mean}=(41)/(6)`

`\text{Mean}=6.833`

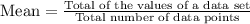
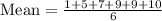
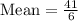
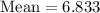
Since our data set has 6 data points, so median will be the average of 3rd and 4th data point.

`\text{Median}=(7+9)/(2)`

`\text{Median}=(16)/(2)`

`\text{Median}=8`

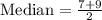
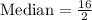
Now let us find mean of new data set after including 75.

`\text{Mean of new data set}=(1+5+7+9+9+10+75)/(7)`

`\text{Mean of new data set}=(116)/(7)`

`\text{Mean of new data set}=16.57`

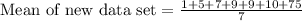
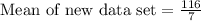
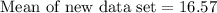
Since our new data set will have 7 data points, so median will be the value of middle or 4th data point, that is 9.

We can see that after adding 75 to our data set mean increased from 6.833 to 16.57, while median increased from 8 to 9. Therefore, the mean and median of new data has increased, but mean increased more.