Question

Lim x-0 3x²/(1-cos5x)

Answer 1

The limit is presented in the following undefined form:

`\displaystyle \lim_(x\to 0)(3x^2)/(1-\cos(5x)) \to (3\cdot 0^2)/(1-\cos(5\cdot 0)) = (0)/(0)`

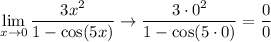
In cases like this, we can use de l'Hospital rule, which states that this limit, if it exists, is the same as the limit of the derivatives of numerator and denominator.

So, we switch

`(f(x))/(g(x))\to(f'(x))/(g'(x))`

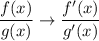
The derivative of the numerator is

`(d)/(dx) 3x^2 = 6x`

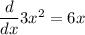
Whereas the derivative of the denominator is

`(d)/(dx) (1-\cos(5x)) = 5\sin(5x)`

So, the new limit is

`\displaystyle \lim_(x\to 0)(6x)/(5\sin(5x)) \to (6\cdot 0)/(5\cdot 0) = (0)/(0)`

So, it would seem that we didn't solve anything, but indeed we have! Recall the limit

`\displaystyle \lim_(x\to 0) (ax)/(\sin(bx)) = (a)/(b)`

to conclude that the limit converges to \dfrac{6}{25} [/tex]

Answer 2

Without using L'Hopital's rule:

`(3x^2)/(1-\cos5x)\cdot(3x^2(1+\cos5x))/((1-\cos5x)(1+\cos5x))=(3x^2(1+\cos5x))/(1-\cos^25x)=(3x^2(1+\cos5x))/(\sin^25x)`

Recall that
`\lim\limits_(x\to0)(5x)/(\sin5x)=1`. Then we have

`\displaystyle\frac3{25}\left(\lim_(x\to0)(5x)/(\sin5x)\right)^2\lim_(x\to0)(1+\cos5x)`

The
`\sin` limit is 1 and the
`\cos` limit is 2, so the final limit is
`\frac6{25}`.