8. What is the domain of (x)/(x^(2) +20x+75) ? Hint: try factoring the polynomial. 9. What is the domain and range of √(13x-7)+1 ? Please hurry! I really need help with this!

Question

8. What is the domain of
`(x)/(x^(2) +20x+75)` ? Hint: try factoring the polynomial.

9. What is the domain and range of
`√(13x-7)+1` ?

Please hurry! I really need help with this!

Answer 1

8. Domain: (-∞, -15) ∪ (-15, -5) ∪ (-5, ∞)

9. Domain: [7/13, ∞)

Range: [1, ∞)

Explanation:

Question 8

Given rational function:

`f(x)=(x)/(x^2+20x+75)`

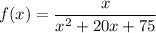
Factor the denominator of the given rational function:

`\implies x^2+20x+75`

`\implies x^2+5x+15x+75`

`\implies x(x+5)+15(x+5)`

`\implies (x+15)(x+5)`

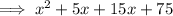
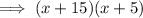
Therefore:

`f(x)=(x)/((x+15)(x+5))`

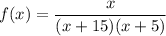
Asymptote: a line that the curve gets infinitely close to, but never touches.

The function is undefined when the denominator equals zero:

`x+15=0 \implies x=-15`

`x+5=0 \implies x=-5`

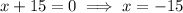
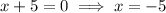
Therefore, there are vertical asymptotes at x = -15 and x = -5.

Domain: set of all possible input values (x-values)

Therefore, the domain of the given rational function is:

(-∞, -15) ∪ (-15, -5) ∪ (-5, ∞)

---------------------------------------------------------------------------------

Question 9

Given function:

`f(x)=√(13x-7)+1`

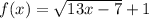
Domain: set of all possible input values (x-values)

As the square root of a negative number is undefined:

`\implies 13x-7\geq 0`

`\implies 13x\geq 7`

`\implies x\geq (7)/(13)`

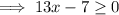
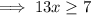
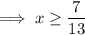
Therefore, the domain of the given function is:

`\left[(7)/(13),\infty\right)`

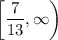
Range: set of all possible output values (y-values)

`\textsf{As }\:√(13x-7)\geq 0`

`\implies √(13x-7)+1\geq 1`

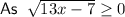
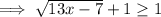
Therefore, the range of the given function is:

[1, ∞)