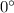Question

Which of the following is a solution to 2cos2x − cos x − 1 = 0?

A. 0° B. 150° C. 180° D. 210°

Answer 1

The correct answer option is A. 0°.

Explanation:

We are given a quadratic equation in cos which is factored in the same way like usual quadratic equation is factored:

`2cos^2x - cos x - 1 = 0`

This can be factorized and can also be written as:

`2cos^2x - 2cosx + cosx - 1 = 0`

or

`2cos x (cos x - 1) + 1(cos x - 1) = 0`

`(2cos x + 1) (cos x - 1) = 0`

`2xcos+1=0` or
`cos x-1=0`

`cos x = -(1)/(2)` or
`cos x = 1`

`x = 120` or
`x = 0`

Therefore, the correct answer option is A. 0°.

Answer 2

Option A is correct.

Solution for the given equation is,
`x = 0^(\circ)`

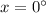
Explanation:

Given that :
`2\cos^2x -\cos x -1 =0`

Let
`\cos x =y`

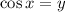
then our equation become;

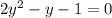`2y^2-y-1= 0` .....[1]

A quadratic equation is of the form:

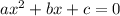`ax^2+bx+c =0`.....[2] where a, b and c are coefficient and the solution is given by;

`x = (-b\pm √(b^2-4ac))/(2a)`

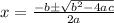
Comparing equation [1] and [2] we get;

a = 2 b = -1 and c =-1

then;

`y = (-(-1)\pm √((-1)^2-4(2)(-1)))/(2(2))`

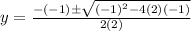
Simplify:

`y = ( 1 \pm √(1+8))/(4)`

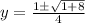
or

`y = ( 1 \pm √(9))/(4)`

`y = ( 1 \pm 3)/(4)`

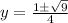
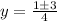
or

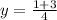`y = (1+3)/(4)` and
`y = (1 -3)/(4)`

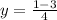
Simplify:

y = 1 and
`y = -(1)/(2)`

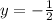
Substitute y = cos x we have;

`\cos x = 1`

⇒
`x = 0^(\circ)`

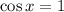
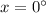
and

`\cos x = -(1)/(2)`

⇒
`x = 120^(\circ) \text{and} x = 240^(\circ)`

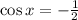
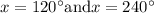
The solution set:
`\{0^(\circ), 120^(\circ) , 240^(\circ)\}`

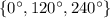
Therefore, the solution for the given equation
`2\cos^2x -\cos x -1 =0` is,
`0^(\circ)`