Question

Which statement(s) is (are) correct?

Poly is working on the probabilities of each food option being selected in her card game. Remember, a standard deck of 52 playing cards contains 4 suits (hearts, diamonds, clubs, and spades), and each suit contains 13 cards, labeled 2 through 10, as well as jack, queen, king, and ace. Hearts and diamonds are red, and spades and clubs are black. The face cards are jacks, queens, and kings.

The rules for drawing a card from a standard deck of 52 cards are as follows.

- If the card is a king, Gourmando eats cured pasta & bear.
- If the card is a 3 ,Gourmando eats baked cucumber & lime mutton.
- If the card is a face card, Gourmando eats poached fennel & lemon alligator.
- If the card is red, Gourmando eats pressure-cooked mushroom & garlic chicken.
- If the card is diamond, Gourmando eats a praline wafer.
- If the card is ace, Gourmando eats gooseberry & passion fruit cheesecake.
- If the card is black, Gourmando eats an oven-baked apple & lavender calzone.

Statements:

The probability of choosing cured pasta & bear is greater than the probability of choosing baked cucumber & lime mutton.

The probability of choosing gooseberry & passion fruit cheesecake is greater than the probability of choosing poached fennel & lemon alligator.

The probability of choosing a praline wafer is greater than the probability of choosing poached fennel & lemon alligator.

The probability of choosing pressure-cooked mushroom & garlic chicken and the probability of choosing an oven-baked apple & lavender calzone are the same.

The probability of choosing pressure-cooked mushroom & garlic chicken and the probability of choosing a praline wafer are the same.

Answer 1

statements 3 and 4 are correct.

Explanation:

(1)

The probability of choosing cured pasta and bear= probability that the card is king.

Hence, The probability of choosing cured pasta and bear=
`(4)/(52)=(1)/(13)`

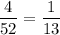
Probability of choosing baked cucumber and lime mutton=probability that the card is 3.

as there are 4 cards that are '3'.

Hence Probability of choosing baked cucumber and lime mutton=
`(4)/(52)=(1)/(13)`

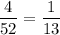
as both the probabilities are equal.

Hence statement 1 is incorrect.

(2)

The probability of choosing gooseberry & passion fruit cheesecake= Probability taht the card is ace.

as there are 4 cards which are ace out of 52 cards.

Hence, The probability of choosing gooseberry & passion fruit cheesecake=
`(4)/(52)=(1)/(13)`

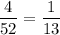
probability of choosing poached fennel & lemon alligator=Probability that the card is a face card.

As there are 12 face cards out of 52 cards.

Hence, probability of choosing poached fennel & lemon alligator=
`(12)/(52)=(3)/(13)`

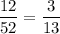
Hence, the probability of choosing gooseberry and passion fruit cheesecake is smaller than the probability of choosing poached fennel & lemon alligator.

Hence statement 2 is false.

(3)

The probability of choosing a praline wafer=probability that the card is a diamond.

as there are 13 diamond cards out of 52 cards.

The probability of choosing a praline wafer=
`(13)/(52)=(1)/(4)`

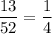
the probability of choosing poached fennel & lemon alligator=Probability that the card is a face card.

As there are 12 face cards out of 52 cards.

Hence, probability of choosing poached fennel & lemon alligator=
`(12)/(52)=(3)/(13)`

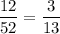
Hence, The probability of choosing a praline wafer is greater than the probability of choosing poached fennel & lemon alligator.

Hence statement 3 is correct.

(4)

The probability of choosing pressure-cooked mushroom & garlic chicken =probability that the card is red.

As there are 26 red cards out of 52 cards.

Hence,

The probability of choosing pressure-cooked mushroom & garlic chicken =
`(26)/(52)=(1)/(2)`

probability of choosing an oven-baked apple & lavender calzone =probability that the card is black.

As there are 26 red cards out of 52 cards.

Hence, probability of choosing an oven-baked apple & lavender calzone=
`(26)/(52)=(1)/(2)`

Hence, The probability of choosing pressure-cooked mushroom & garlic chicken and the probability of choosing an oven-baked apple & lavender calzone are the same.

Hence statement 4 is true.

(5)

The probability of choosing pressure-cooked mushroom & garlic chicken =probability that the card is red.

As there are 26 red cards out of 52 cards.

Hence,

The probability of choosing pressure-cooked mushroom & garlic chicken =
`(26)/(52)=(1)/(2)`

the probability of choosing a praline wafer=probability that the card is a diamond.

as there are 13 diamond cards out of 52 cards.

The probability of choosing a praline wafer=
`(13)/(52)=(1)/(4)`

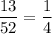
Hence, the probability of choosing pressure-cooked mushroom & garlic chicken and the probability of choosing a praline wafer are not same.

Hence, statement 5 is not correct.