Answer:
The series has 25 terms.
Explanation:
You could just diligently count, but it looks much better if you use the formula for the n-th term of an arithmetic series like this:

so the k=0 term is 15, k=1 is 18, etc. Now we solve an equation as follows:
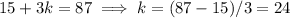
so the last term (87) occurs for k=24, which means, including the 0-th term, there are 25 terms in this series.
The advantage of this method is that it would work for very very long series just as nicely, like 15+18+21+...+ 3015, 3018 (where the diligent method would just be way too boring)