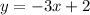Answer:
AB:
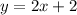
CB:
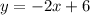
CD:
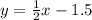
DA:
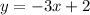
Explanation:
So when it's saying y = __ x + __ it's asking for the slope-intercept form. This is given as y=mx+b where m is the slope and b is the y-intercept. m is the slope because as x increases by 1, the y-value will increase by m, which is by definition what the slope is
 how much the function "rises" as x "runs".
how much the function "rises" as x "runs".
AB: See how it "rises" by 2 and only "runs by 1", thus the slope is 2/1 or 2. the last part is the y-intercept, which is the value of y when the line crosses the y-axis. If you look at the graph when it "crosses" the y-axis it's y-value is 2. So you have the equation:
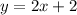
CB: See how it "goes down" by 4 and "runs" by 2, thus the slope is -4/2 or -2. The y-intercept isn't shown on the graph but you can calculate that by substituting known values into the slope-intercept form. So we know so far y=-2x+b since the slope was calculated, and we can take any point on the line to calculate b, for this example I'll take the point C which is (3, 0) which is (x, y) and I'll plug that in
Plug values in:
0 = -2(3) + b
0 = -6 + b
6 = b
This gives you the complete equation:
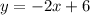
CD: see how it only "rises" by 1 but "runs" by 2, thus the slope is 1/2. The y-intercept isn't shown on the graph but you can calculate it by substituting a point into the equation For this example I'll use point C (3, 0)
0 = 3(1/2) + b
0 = 1.5 + b
-1.5 = b
This gives you the complete equation:
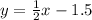
DA: see how it "decreases" by 3 but "runs" by 1, thus the slope is -3/1 or -3. The y-intercept is known and is at (0, 2) so now we plug these values in to get the equation: