Question

Nicole wants to know the height of the snow sculpture but its too tall to measure. Nicole measured the shadow of the snow sculptures highest point to be 10 feet long. At the dame time of day Nicoles shadow was 40 inches long. If Nicole is five feet long what is the height of the snow sculplture?

Answer 1

Answer: 15 feet.

Explanation:

Let Line segment AB shows the actual height of the snow sculpture , line segment DE shows the height of Nicole and BC is the height of the shadow of the Sculpture,

Then According to the question,

DE = 5 feet , BC = 10 feet and CE = 40 inches = 10/3 feet

In triangles, ACB and DCE,

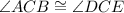`\angle ACB \cong \angle DCE`( reflexive)

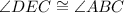`\angle DEC \cong \angle ABC` ( Right angles)

Thus, by AA similarity postulate,

Triangles ACB and DCE are similar.

⇒
`(AB)/(DE) = (CB)/(CE)`

`(AB)/(5) = (10)/(10/3)`

`(AB)/(5) = 3`

`AB = 15`

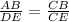
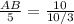
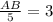
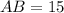
Therefore, the height of sculpture = 15 feet.

Answer 2

15 feet.

Explanation:

We have been given that Nicole measured the shadow of the snow sculptures highest point to be 10 feet long. At the same time of day Nicole's shadow was 40 inches long. Nicole is five feet long.

We will use proportions to solve our given problem as proportions states that two fractions are equal.

`\frac{\text{The height of the snow sculpture}}{\text{The Height of shadow of snow sculpture}}=\frac{\text{Nicole's height}}{\text{Height of Nicole's shadow}}`

Let us convert given measurements from feet to inches.

1 feet = 12 inches.

10 feet = 10*12 inches = 120 inches.

5 feet =5*12 = 60 inches

`\frac{\text{The height of the snow sculpture}}{120}=(60)/(40)`

Let us multiply both sides of our equation by 120.

`\frac{\text{The height of the snow sculpture}}{120}*120=(60)/(40)*120`

`\text{The height of the snow sculpture}=60*3`

`\text{The height of the snow sculpture}=180`

So the height of the snow sculpture is 180 inches. Let us convert our final answer to feet by dividing 180 by 12.

`\text{The height of the snow sculpture}=\frac{180\text{ inches}}{12}* \frac{\text{feet}}{\text{inches}}`

`\text{The height of the snow sculpture}=\frac{180\text{ inches}}{12}* \frac{\text{feet}}{\text{inches}}`

`\text{The height of the snow sculpture}=15\text{ feet}`

Therefore, the height of the snow sculpture is 15 feet.