Question

What are the exact steps to solve for the x-intercepts of f(x)= −4x2 + 4x + 8? What about −9 = x2 + 6x? Please explain thoroughly

Answer 1

x-intercepts: (-1, 0) and (2, 0)

x-intercept: (-3, 0)

Explanation:

Given quadratic function:

`f(x)=-4x^2+4x+8`

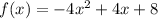
The x-intercepts of a quadratic function are the points at which the curve crosses the x-axis ⇒ when y = 0

Therefore, to find the x-intercepts of the given function, set the function to zero:

`\implies -4x^2+4x+8=0`

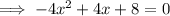
Factor out -4:

`\implies -4(x^2-x-2)=0`

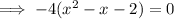
Divide both sides by -4

`\implies x^2-x-2=0`

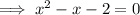
Rewrite the middle term as -2x + x:

`\implies x^2-2x+x-2=0`

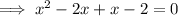
Factor the first two terms and the last two terms separately:

`\implies x(x-2)+1(x-2)=0`

Factor out the common term (x - 2):

`\implies (x+1)(x-2)=0`

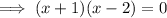
Zero Product Property: If a ⋅ b = 0 then either a = 0 or b = 0 (or both).

Using the Zero Product Property, set each factor equal to zero and solve for x (if possible):

`\begin{aligned}(x+1) & = 0 & \quad \textsf{ or } \quad \quad (x-2) & = 0\\\implies x & = -1 & \implies x & = 2\end{aligned}`

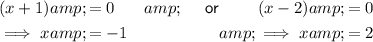
Therefore, the x-intercepts are (-1, 0) and (2, 0).

---------------------------------------------------------------------------------------

Given quadratic equation:

`-9 = x^2 + 6x`

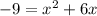
Add 9 to both sides:

`\implies x^2+6x+9=0`

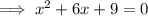
Rewrite the middle term as 3x + 3x:

`\implies x^2+3x+3x+9`

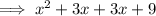
Factor the first two terms and the last two terms separately:

`\implies x(x+3)+3(x+3)=0`

Factor out the common term (x + 3):

`\implies (x+3)(x+3)=0`

`\implies (x+3)^2=0`

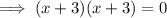
Square root both sides:

`\implies (x+3)=0`

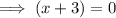
Solve for x:

`\implies x=-3`

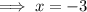
Therefore, the x-intercept is (-3, 0).

As the function has a repeated factor (multiplicity of two), the curve will touch the x-axis at (-3, 0) and bounce off.