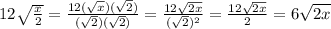Answer:
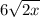
Explanation:
1. You have the following expression given in the problem above:
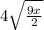
2. Remove the perfects squares from the square root:
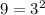
Then:
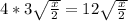
3. Now, rationalize the denominator, because it cotains an square root. Multiply the numerator and the denominator by
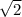 and simplify, as following:
and simplify, as following: