Question

A sundae requires 3 ice-cream scoops and 4 strawberries, and a milkshake requires 2 ice-cream scoops and 6 strawberries. Ramses wants to make sundaes and milkshakes with at most 25 ice-cream scoops and 37 strawberries. Let's form a system of inequalities to represent his conditions. Let x denote the number of sundaes he makes and y the number of milkshakes he makes.

Maximum number of sundaes possible:

Maximum number of milkshakes possible:

Combination that uses the most of both Ice-cream and Strawberries:

Answer 1

System of inequalities:

`3x+2y \leq 25` ,
`4x+6y \leq 37`

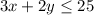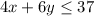
1) Maximum number of sundaes possible = 9

2) Maximum number of milkshakes possible = 6

3) Combination that uses the most of both Ice-cream and Strawberries = 7 scoop of ice-cream and 1 scoop of strawberries.

Explanation:

Given : A sundae requires 3 ice-cream scoops and 4 strawberries, and a milkshake requires 2 ice-cream scoops and 6 strawberries.

Ramses wants to make sundaes and milkshakes with at most 25 ice-cream scoops and 37 strawberries.

Let x denote the number of sundaes he makes and y the number of milkshakes he makes.

First we represent in tabular form,

Sundae(x) Milkshake(y) Total

Ice-cream 3 2 3x+2y

Strawberries 4 6 4x+6y

→System of inequalities:

Sundaes and milkshake with at most 25 ice-cream scoops=
`3x+2y \leq 25`

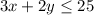
Sundaes and milkshakes with at most 37 strawberries =
`4x+6y \leq 37`

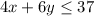
→ Plotting the equations in the graph (figure attached)

1) Maximum number of sundaes possible:

Maximum no. of sundaes possible when y=0

From the graph y=0 at x=9.25

Therefore, Maximum number of sundaes possible is 9

2) Maximum number of milkshakes possible:

Maximum no. of milkshakes possible when x=0

From the graph x=0 at y= 6.167

Therefore, Maximum number of milkshakes possible is 6

3) Combination that uses the most of both Ice-cream and Strawberries:

Combination of both is possible there is a intersection of both the equation

From the graph intersection point is x=7.6 and y=1.1

Therefore, Combination that uses the most of both Ice-cream and Strawberries = 7 scoop of ice-cream and 1 scoop of strawberries.

Answer 2

Answer: for the people who's question is a little different and on Khan Academy...

inequality that represents the condition based on the number of ice cream scoops: 3S+2M≤25

inequality that represents the condition based on the number of strawberries:

4S+6M≤37

Explanation:

We are given that a sundae requires 3 ice-cream scoops, and a milkshake requires 2 ice-cream scoops.

How can we express the total number of ice-cream scoops Ramses expects to use?

The number of ice-cream scoops required to make S sundaes is 3S, S, and the number of ice-cream scoops required to make M milkshakes is 2M. Therefore, the total number of ice-cream scoops Ramses expects to use is 3S+2M.

We are also given that Ramses has at most 25 ice-cream scoops. Let's use this to create the appropriate inequality:

3S+2M≤25

Similarly, the number of strawberries required to make S sundaes is 4S, and the number of strawberries required to make M milkshakes is 6M. Since we are also given that Ramses has at most 37 strawberries, this is the appropriate inequality:

4S+6M≤37

proof lol: