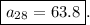Question

Thank you for who can ever answer this

Answer 1

The 28th term is
`\boxed{63.8}.`

Explanation:

Let
`a_n` denote the
`n`th term of the sequence.

We can start by noticing that:

`a_2 - a_1 = a_3 - a_2 = a_4 - a_3 = 2.6 = r,`

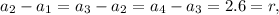
which means that this sequence is actually an arithmetic progression. We know that the
`n`th term of these sequences is always:

`a_n = a_1 + r(n-1).`

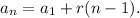
This sequence in particular is given by:

`a_n = -6.4 + 2.6 (n-1).`

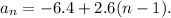
To find the 28th term, we simply set
`n=28`:

`a_(28) = -6.4 + 2.6 (28-1) = -6.4 + 2.6 * 27 = -6.4 + 70.2 = 63.8.`

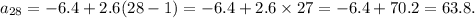
So we finally get:

`\boxed{a_(28) = 63.8}.`