Question

Determine algebraically whether the function is even, odd, or neither even nor odd. (2 points)

f(x) = -3x4 - 2x - 5

Answer 1

The function f(x) is neither even nor odd.

Explanation:

The given function is

`f(x) = -3x^4 - 2x - 5`

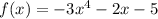
A function is called an even function if

`f(-x) = f(x)`

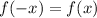
A function is called an odd function if

`f(-x) = -f(x)`

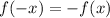
Substitute x=-x in the given function, to check whether the function is even, odd, or neither even nor odd.

`f(-x) = -3(-x)^4 - 2(-x) - 5`

`f(-x) = -3(x)^4 + 2(x) - 5`

`f(-x) \\eq f(x)`

`f(-x) \\eq -f(x)`

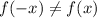
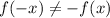
Therefore the function f(x) is neither even nor odd.

Answer 2

f(x) is neither odd nor even function

Explanation:

we are given

`f(x)=-3x^4-2x-5`

Firstly, we will find f(-x)

we can replace x as -x

we get

`f(-x)=-3(-x)^4-2(-x)-5`

now, we can simplify it

`f(-x)=-3x^4+2x-5`

we can see that

it is neither equal to f(x) nor -f(x)

we know that

For even:

`f(-x)=f(x)`

For odd:

`f(-x)=-f(x)`

so, f(x) is neither odd nor even function