Question

What type of conic is given by the equation 4x^2+9y^2=36

Answer 1

This is equation of ellipse

Explanation:

we are given

`4x^2+9y^2=36`

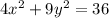
We can see that right side is 36

so, we can make right side as 1 by dividing both sides by 36

`(4x^2+9y^2)/(36) =(36)/(36)`

`(4x^2+9y^2)/(36) =1`

`(4x^2)/(36)+(9y^2)/(36) =1`

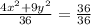
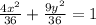
we can simplify it

`(x^2)/(9)+(y^2)/(4) =1`

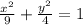
we can rewrite it as

`(x^2)/(3^2)+(y^2)/(2^2) =1`

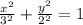
now, we can compare it with standard equation of ellipse

`((x-h)^2)/(a^2)+((y-k)^2)/(b^2) =1`

we can see that both equations are similar

so, this is equation of ellipse