Answer:
C. The situation represents a geometric sequence because the successive y-values have a common ratio of 1.05
Explanation:
We are given
In 2006, 5,200 highway accidents were recorded in a city
The number of highway accidents increases by 5% every year
Let y represent the number of highway accidents x years since 2006
Since, 5% is increasing every year of previous number
so, this is geometric series
In 2006 :
x=0
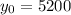
now, we can use formula
i=5%=0.05

now, we can plug values
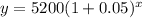
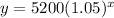
now, we can compare with nth terms of geometric series
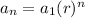
where r is the common ratio
so, we can find r
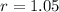
so, common ratio is 1.05