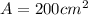Answer:
200 square centimeters
Explanation:
The area of a triangle can be calculated using the formula:
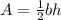 where b is the base and h is the height. So if the base is 16 cm and the height if 25 cm you simply plug the values into the equation to find the area
where b is the base and h is the height. So if the base is 16 cm and the height if 25 cm you simply plug the values into the equation to find the area
Plug Values In:
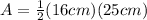
Multiply 16 cm and 25 cm:
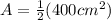
Multiply by 0.5 (or technically divide by 2)