Answer:
All zeros are
x=-10 , x=-5 , x=5
Explanation:
we are given function as
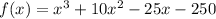
we are given one of zero is x=-10
we have to use Remainder theorem
we can find all possible factor of 250

so, we will check zeros at x=-5 and x=5
At x=-5:
we can plug x=-5
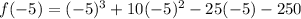
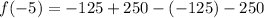
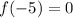
At x=5:
we can plug x=5

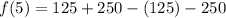

So, other zeros are
x=-5 and x=5
All zeros are
x=-10 , x=-5 , x=5