Question

Given:

RSTU is a parallelogram.



TRS

RXS
RTU
RXU

See Picture

Answer 1

Option B is correct.

`\triangle RST \cong \triangle TUR`

Explanation:

Given: RSTU is a parallelogram.

By definition of parallelogram, two pairs of opposite sides are congruent in length.

⇒
`TU \cong RS` and
`TS \cong RU`

In triangle RST and triangle TUR

`RS \cong TU` [Side]

`TS \cong RU` [Side]

`RT \cong RT` [Common side]

SSS(Side-Side-Side) postulates states that if three sides of one triangle are congruent to three sides of other triangle, then the triangles are congruent.

then, by SSS postulates we have;

`\triangle RST \cong \triangle TUR`

Answer 2

`\Delta TRS \cong \Delta RTU`

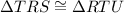
Step-by-step explanation:

We have been given a graph of a parallelogram and we are asked to find which triangle is congruent to triangle TRS.

Since we know that the opposite sides of a parallelogram are equal, so TU = RS.

Since the alternate interior angles formed by two parallel and a transversal is equal. We can see that line TU is parallel to line RS and TR will be our transversal, therefore, angles formed inside the parallel lines and on the opposite sides of transversal will be equal.

By alternate interior angles:
`m\angle TRS=m\angle RTU`

We can see that in triangle TRS and RTU segment RT equals to itself.

Therefore, by SAS congruence postulate
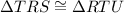`\Delta TRS \cong \Delta RTU` and option B is the correct choice.