Question

Find the perimeter of th image below

Answer 1

26.13 units.

Explanation:

We are asked to find the perimeter of the given figure.

First of all we will find the length of each line segment using distance formula.

`\text{Distance}=√((x_2-x_1)^2+(y_2-y_1)^2)`

`\text{Distance between Q and R}=√((2-4)^2+(0-5)^2)`

`\text{Distance between Q and R}=√((-2)^2+(-5)^2)`

`\text{Distance between Q and R}=√(4+25)`

`\text{Distance between Q and R}=√(29)`

`\text{Distance between R and S}=√((4-8)^2+(5-7)^2)`

`\text{Distance between R and S}=√((-4)^2+(-2)^2)`

`\text{Distance between R and S}=√(16+4)`

`\text{Distance between R and S}=√(20)`

`\text{Distance between S and T}=√((8-6)^2+(7-4)^2)`

`\text{Distance between S and T}=√((2)^2+(3)^2)`

`\text{Distance between S and T}=√(4+9)`

`\text{Distance between S and T}=√(13)`

`\text{Distance between T and U}=√((6-10)^2+(4-3)^2)`

`\text{Distance between T and U}=√((-4)^2+(1)^2)`

`\text{Distance between T and U}=√(16+1)`

`\text{Distance between T and U}=√(17)`

`\text{Distance between U and Q}=√((10-2)^2+(3-0)^2)`

`\text{Distance between U and Q}=√((8)^2+(3)^2)`

`\text{Distance between U and Q}=√(64+9)`

`\text{Distance between U and Q}=√(73)`

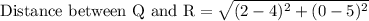
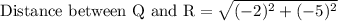
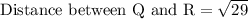
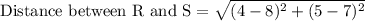
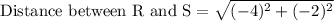
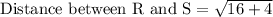
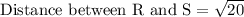
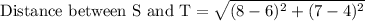
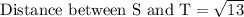
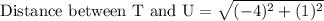
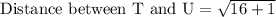
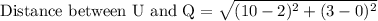
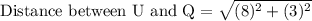
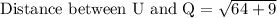
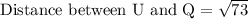
Let us add all the lengths to find the perimeter of our given figure.

`\text{Perimeter}=√(29)+√(20)+√(13)+√(17)+√(73)`

`\text{Perimeter}=26.1299614085332644\approx 26.13`

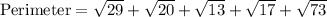
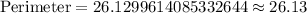
Therefore, the perimeter of our given image will be 26.13 units.