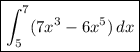Question

Isn't the series here divergent? doesn't that mean it cannot be represented as a riemann sum

Answer 1

No issues with convergence here. If you actually expand the summand you can use the well-known Faulhaber formulas to compute the sum.

`\displaystyle \sum_(i=1)^n 1 = n`

`\displaystyle \sum_(i=1)^n i = \frac{n(n+1)}2`

`\displaystyle \sum_(i=1)^n i^2 = \frac{n(n+1)(2n+1)}6`

`\displaystyle \sum_(i=1)^n i^3 = \frac{n^2(n+1)^2}4`

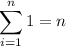
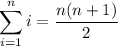
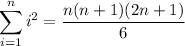
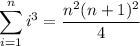
and so on. You would end up with

`\displaystyle L_n = \frac2n * (96-8796n^2+40283n^3-49458n^4)/(n^3)`

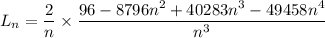
As
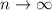`n\to\infty`, we have
`L_n\to-98916`.

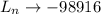Now, when
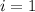`i=1`, the first term of the sum is

`7(5+0)^3 - 6(5+0)^5`

so the left endpoint of the first subinterval is
`a=5`.

At the other end, when
`i=n`, the last term of the sum is

`7\left(5+\frac{2(n-1)}n\right)^3 - 6\left(5+\frac{2(n-1)}n\right)^5`

which converges to

`7(5+2)^3 - 6(5+2)^5`

so the left endpoint of the last subinterval converges to
`b=5 + 2 = 7`.

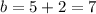From here it's quite clear that
`f(x)=7x^3-6x^5`. So, the Riemann sum converges to the definite integral

`\boxed{\displaystyle \int_5^7 (7x^3 - 6x^5) \, dx}`