Question

The area of a rhombus can be evaluated using the formula 1/2 d1d2 , where d1 represents the measure of one of its diagonals and d2 represents the measure of its other diagonal. When d1 is a terminating decimal and d2 is a repeating decimal, what can be concluded about the area of the rhombus?

Answer 1

Area of the rhombus will be a repeating decimal.

Explanation:

In a terminating decimals, numbers get terminated after decimal like

1/4 = 0.25

while in repeating decimals, numbers get repeated after decimal like

1/3 = 0.33333

When we multiply two decimals which are repeating and terminating decimals the result will be a repeating decimal.

Therefore area of the rhombus will be a repeating decimal.

Answer 2

Area of the rhombus is a is a repeating decimal or a rational number.

Explanation:

The area of a rhombus can be evaluated using the formula

`Area=(1)/(2)d_1d_2`

where, d1 represents the measure of one of its diagonals and d2 represents the measure of its other diagonal.

Repeating decimal: After decimal the same sequence of digits repeats indefinitely. For example 2.333.. and 5.666.. etc.

Terminating decimal: It is a decimal number with a finite number of digits after the decimal. For example: 2.34 and 6.872 etc.

Rational numbers: A number which can be defined as p/q , where p and q are integers and q≠0, then the number is called a rational number.

Repeating decimal and Terminating decimal are rational numbers.

Product of two or more rational numbers is a rational number.

Product of a repeating decimal and terminating decimal is always a repeating decimal.

Let
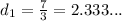`d_1=(7)/(3)=2.333...` and
`d_2=(11)/(4)=2.75`

`Area=(1)/(2)((7)/(3))((11)/(4))`

`Area=(77)/(24)`

`Area=3.20833333333`

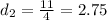
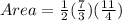
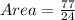
Therefore, the area of the rhombus is a is a repeating decimal or a rational number.