Question

Type the correct answer in the box. Use numerals instead of words. If necessary, use / for the fraction bar. While testing a new vaccine, a lab technician noticed that the number of bacteria reduced by half every minute. How long does it take for 3,000 bacteria to reduce to 375? It takes minutes for the number of bacteria to reduce from 3,000 to 375.

Answer 1

3 minutes

Explanation:

First find the number of half lifes' there is from 3000 to 375.

3000 ÷ 2 = 1500 ⇒⇒⇒⇒ 1

1500 ÷ 2 = 750 ⇒⇒⇒⇒⇒ 2

750 ÷ 2 = 375 ⇒⇒⇒⇒⇒ 3

There are 3 half lives' meaning it reduces 3 times from 3000 to 375.

Each reduction takes 1 minutes.

The total time to reduce from 3000 to 375 is:

3 × 1 = 3 minutes.

Answer 2

3 minutes

Explanation:

It says that the number of bacteria reduces by half every minute.

So we can represent this situation by the equation:

`x=x_(0)*((1)/(2))^(n)`

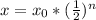
where x₀ is the original number of bacteria and x is the number of bacteria that remains after n minutes.

Plugin x₀ = 3000 and x = 375 into the above formula

`375=3000*((1)/(2) )^(n)`

Dividing both sides by 3000

`(375)/(3000)=(3000)/(3000)*((1)/(2) )^(n)`

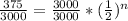
Cancel out 3000's on the top and bottom of the right side

`(375)/(3000)=((1)/(2) )^(n)`

Simplifying the fraction
`(375)/(3000)`

`(1)/(8)=((1)/(2) )^(n)`

`(1)/(2)*(1)/(2)*(1)/(2)=((1)/(2) )^(n)`

`((1)/(2) )^(3)=((1)/(2) )^(n)`

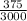
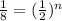
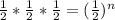
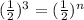
Comparing the exponents on both sides, we get

n=3

So, it will take 3 minutes for to reduce the number of bacteria from 3000 to 375.