Answer: 20 feet by 20 feet.
Explanation:
1. You know that
 is the original measure of one side. Since it is a square, all its sides are equal.
is the original measure of one side. Since it is a square, all its sides are equal.
2. Therefore, to solve the problem you only need to solve for
 , as you can see below:
, as you can see below:
- You have that:
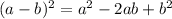
- Then, you obtain the following quadratic equation:
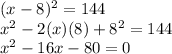
- Apply the Quadratic formula to solve it:
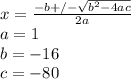
- Then, you obtain:

3. The dimensions cannot be negative, therefore, the answer is: 20 feet by 20 feet.