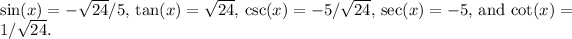Final Answer:
1. The trigonometric ratios for
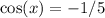 in the third quadrant are:
in the third quadrant are:
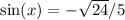
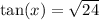
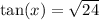
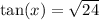
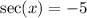
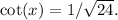
Step-by-step explanation:
Given that
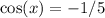 and x is in the third quadrant, we can determine the other trigonometric ratios using the relationships between trigonometric functions. In the third quadrant,
and x is in the third quadrant, we can determine the other trigonometric ratios using the relationships between trigonometric functions. In the third quadrant,
 is negative, and
is negative, and
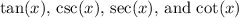 are positive.
are positive.
Using the Pythagorean identity
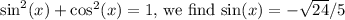 . The tangent
. The tangent
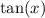 is calculated as
is calculated as
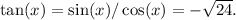
The reciprocal functions are then obtained as
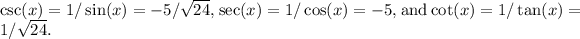 Thus, the complete set of trigonometric ratios for
Thus, the complete set of trigonometric ratios for
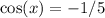 in the third quadrant is
in the third quadrant is