Answer:
The possible test points are -5,-3.5 , -2.5,0,5
Explanation:
Given : The inequality
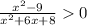 can be factored as
can be factored as
(x + 3)(x - 3) (x + 4)(x + 2) > 0
To find : Which are possible test points?
Solution : The inequality factored as
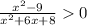
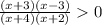
The critical points are defined as when we equation the factor to zero then the value of x is the critical point.
So, x+3=0 ⇒ x=-3
x-3=0 ⇒ x=3
x+4=0 ⇒ x=-4
x+2=0 ⇒ x=-2
The critical points of the given inequality are -4,-3,-2,3
The possible test points are the points except critical points.
Therefore, Out of the given options
The possible test points are -5,-3.5 , -2.5,0,5 as they are not critical points.