Answer:
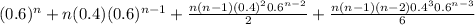
Explanation:
We will use the binomial distribution. Let X be the random variable representing the no. of boxes Hannah buys before betting a prize.
Our success is winning the prize, p =40/100 = 0.4
Then failure q = 1-0.4 = 0.6
Hannah keeps buying cereal boxes until she gets a prize. Then n be no. times she buys the boxes.
P(X ≤ 3) = P(X=0) +P(X=1)+P(X=2)+P(X=3)
=
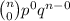 +
+
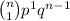 +
+
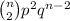 +
+
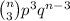
=
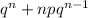 +
+
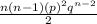 +
+
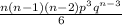
=
(0.4)^(2)0.6^(n-2))/(2) +(n(n-1)(n-2)0.4^(3)0.6^(n-3))/(6)](https://img.qammunity.org/2020/formulas/mathematics/high-school/qic5poklf376fzd6ejh3tupgc96p8b6599.png)