Answer:
Given that:
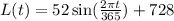
where
L(t) represents the length of each day(in minutes) and t represents the number of days.
Substitute the value of L(t) = 750 minutes we get;
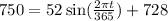
Subtract 728 from both sides we get;
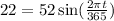
Divide both sides by 52 we get;
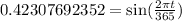
or
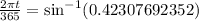
Simplify:
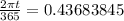
or
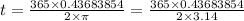
Simplify:
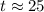 days
days
Therefore, the first day after the spring equinox that the day length is 750 minutes, is 25 days