Answer:
Ethan's string is
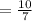 feet longer than Kayla's string.
feet longer than Kayla's string.
Explanation:
Let Ethan's string = x feet
and Kayla's string = y feet
According to question,
Half of Ethan's string is equal to 2/3 of Kayla's string that is,
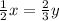
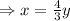 ..............(1)
..............(1)
Also,The total length of their strings is 10 feet that is,
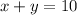
Put value of x from (1),

Solving for y, we get,
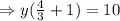
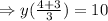
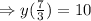
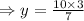
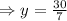
Thus, Length of Kayla's string is
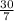 feet.
feet.
and Put value of y in (1) to get value of x,
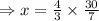

Thus, Length of Ethan's string is
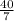 feet.
feet.
Length of Ethan's string is longer than Kayla's string = Length of Ethan's string-Length of Kayla's string.

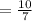
Thus, Ethan's string is
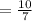 feet longer than Kayla's string.
feet longer than Kayla's string.