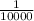Answer:
k=
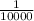
Explanation:
The given equation to us is
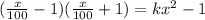
Now the RHS of the equation can be written as
(a-b)(a+b) = a²-b²
So the given equation becomes

Squaring the terms which have square over them
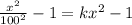
as 100² = 10000 so putting its value
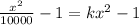
Adding one on both sides of the equation

it becomes
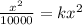
Now to get the value of K we have to divide both side of the equation with x²
so dividing with x² gives
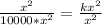
Cutting out the same terms gives us
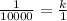
or
k=