Question

PLEASE HELP ASAP!!! CORRECT ANSWERS ONLY PLEASE!!!

Which graph represents the function f(x) = x^2 - 16/x - 4?

Answer 1

Graph B.

Explanation:

Answer 2

Answer: B

Explanation:

`f(x) = (x^2-16)/(x-4)`

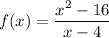
Restriction: denominator cannot equal zero so x - 4 ≠ 0 → x ≠ 4

`f(x) = ((x-4)(x+4))/(x-4) = x + 4`

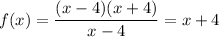
Since the denominator (x - 4) cancelled out, x = 4 is not a vertical asymptote - it is a hole.

f(x) = x + 4 is the simplified function

f(4) = (4) + 4

= 8

So, the hole is at (4, 8)

The graph is the line y = x + 4 with a hole at (4, 8). The only graph that has these attributes is the top right graph, which I call graph B.